ABCDA1B1C1D1 — прямоугольный параллелепипед такой, что AB = 16, AD = 2. Через середины ребер AA1 и BB1 проведена плоскость (см.рис.), составляющая угол 60° с плоскостью основания ABCD. Найдите площадь сечения параллелепипеда этой плоскостью.
Вычислите 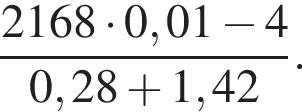
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Объем прямоугольного параллелепипеда ABCDA1B1C1D1 равен 432. Точка P лежит на боковом ребре CC1 так, что CP : PC1 = 2 : 1. Через точку P, вершину D и середину бокового ребра AA1 проведена секущая плоскость, которая делит прямоугольный параллелепипед на две части. Найдите объём меньшей из частей.
Из точки A к окружности проведены касательные AB и AC и секущая AM, проходящая через центр окружности O. Точки B, С, M лежат на окружности (см. рис.). Известно, что BK = 7, AC = 10. Найдите длину отрезка AK.
Пусть a = 3,6; b = 7,8 · 101. Найдите произведение ab и запишите его в стандартном виде.
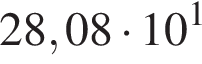
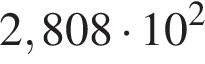
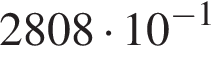

На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Если 16% некоторого числа равны 28, то 60% этого числа равны:
Высоты остроугольного равнобедренного треугольника ABC (AB = BC) пересекаются в точке O. Если высота AD = 15 и AO = 10, то длина стороны AC равна:
Если 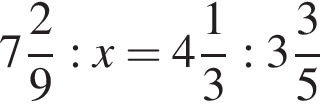 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 200°. Найдите градусную меру меньшего угла.
Если 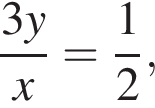 то значение выражения
то значение выражения 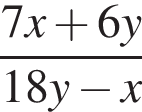 равно:
равно:
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Решением неравенства
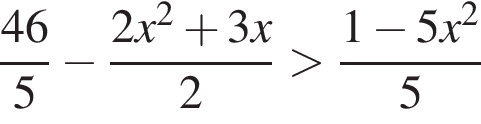
является промежуток:

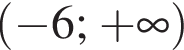
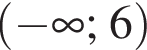
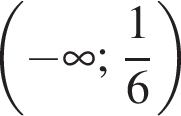
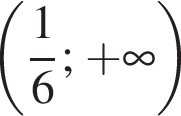
Найдите сумму целых решений неравенства 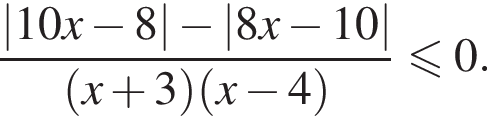
Найдите произведение наименьшего и наибольшего целых решений неравенства 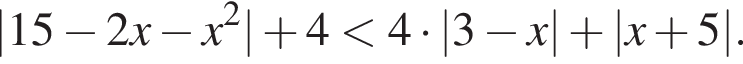
Выразите x из равенства 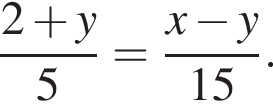
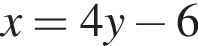
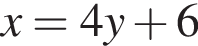


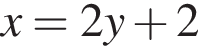
Уравнение 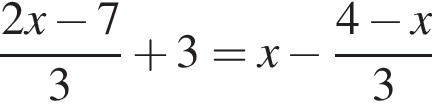 равносильно уравнению:
равносильно уравнению:


Пусть (x1; y1), (x2; y2) — решения системы уравнений 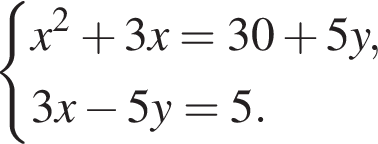
Найдите значение выражения 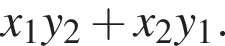
Укажите номер рисунка, на котором показано множество решений системы неравенств 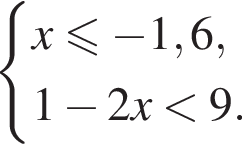
1)
2)
3)
4)
5)
Используя рисунок, определите верное утверждение и укажите его номер.


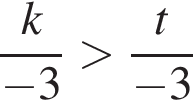
Найдите значение выражения 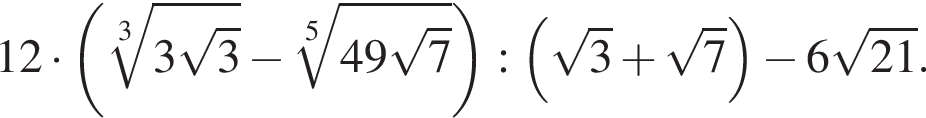
Упростите выражение 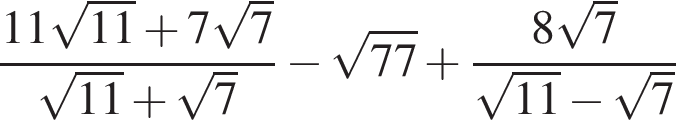
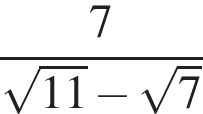
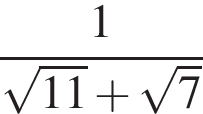
Сумма корней (корень, если он единственный) уравнения 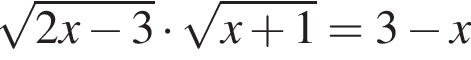 равна (равен):
равна (равен):
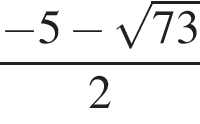
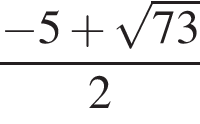
Значение выражения 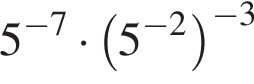 равно:
равно:
Найдите произведение корней уравнения 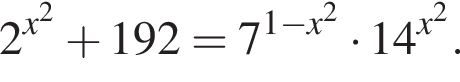
Найдите сумму целых решений неравенства 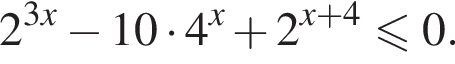
Пусть 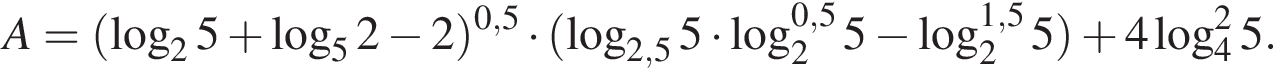
Найдите значение выражения 2A.
Корень уравнения
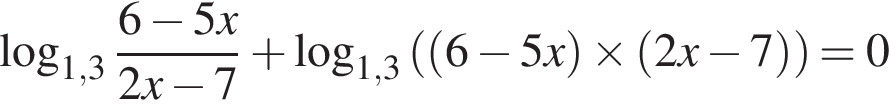
(или сумма корней, если их несколько) принадлежит промежутку:
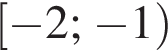
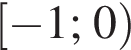
Найдите сумму наименьшего и наибольшего целых решений неравенства 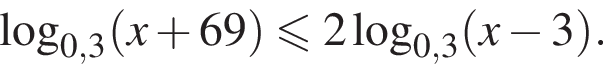
Упростите выражение 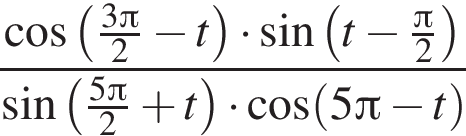
Найдите значение выражения 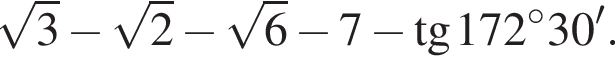
Найдите (в градусах) сумму корней уравнения 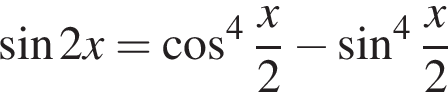 на промежутке [−223°; 333°].
на промежутке [−223°; 333°].
Найдите количество корней уравнения 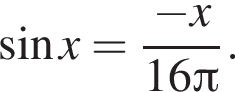
Количество целых решений неравенства 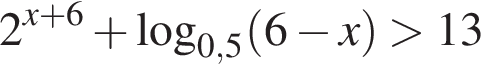 равно ...
равно ...
Геометрическая прогрессия со знаменателем 7 содержит 10 членов. Сумма всех членом прогрессии равна 24. Найдите сумму всех членов прогрессии с четными номерами.
Найдите сумму целых значений x, принадлежащих области определения функции
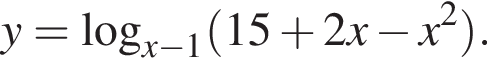
График функции, заданной формулой y = kx + b, симметричен относительно начала координат и проходит через точку A (3; 6). Значение выражения k + b равно:
В рамках акции «Книги — детям» школа получила некоторое количество книг, распределение которых по рубрикам показано на диаграмме: «І» — учебники и учебные пособия, «ІІ» — методические пособия, «ІІІ» — научно-популярная литература, «ІV» — художественная литература (см. рис.). Какое количество учебников и учебных пособий поступило в школу, если книг научно-популярной тематики и методических пособий было 396?
Точки A(−1; 2) и B(2 ;7) — вершины квадрата ABCD. Периметр квадрата равен:
Сумма наибольшего и наименьшего значений функции
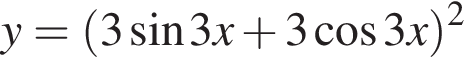
равна:
Собственная скорость катера в 6 раз больше скорости течения реки. Расстояние по реке от пункта A до пункта B плот проплыл за время t1, а катер — за время t2. Тогда верна формула:
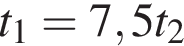
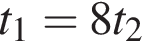
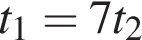
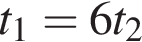
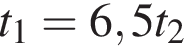
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 5 дм, после чего площадь оставшейся части листа оказалась равной 24 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Строительные бригады №1 и №2 купили соответственно 18 и 19 фундаментных блоков у одного из трех поставщиков, выбрав для себя наиболее дешевый вариант. Стоимость одного блока и условия доставки всей покупки приведены в таблице. Определите, на сколько рублей дороже обошлась эта покупка с доставкой одной из бригад. Ответ запишите в рублях.
| Поставщик | Стоимость (тыс. руб. за 1 шт.) | Стоимость доставки (тыс. руб. за всю покупку) | Специальное предложение |
|---|---|---|---|
| 1 | 205 | 1850 | — |
| 2 | 240 | 1950 | Доставка со скидкой 50 %, если сумма заказа превышает 4,5 млн. бел. рублей |
| 3 | 275 | 2050 | Доставка бесплатно, если сумма заказа превышает 5 млн. бел. рублей |
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.


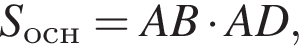 таким образом:
таким образом: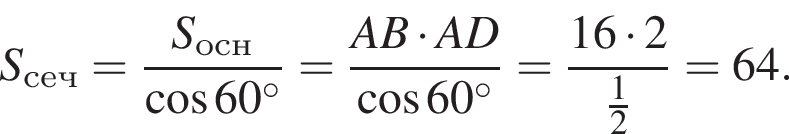
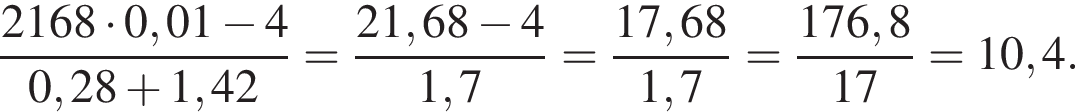
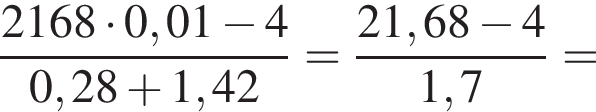
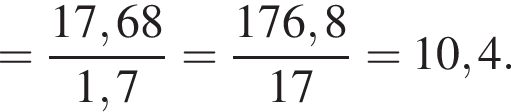
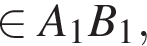 проведем KP||OM, K
проведем KP||OM, K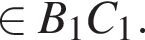 Таким образом, MNKPD — искомое сечение.
Таким образом, MNKPD — искомое сечение.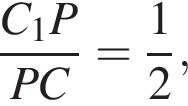 тогда
тогда 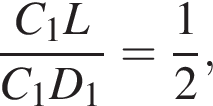 тогда
тогда 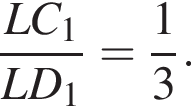
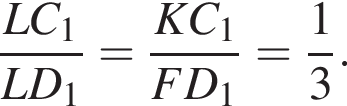 Аналогично находим отношение
Аналогично находим отношение 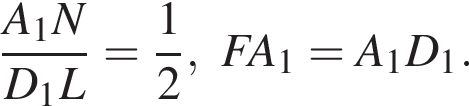
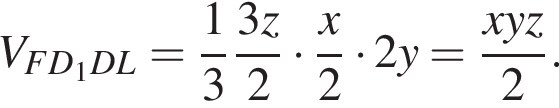
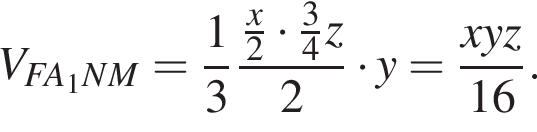
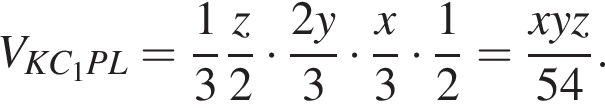
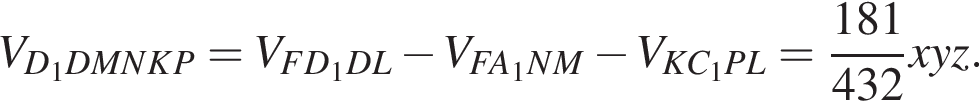
 следовательно, это искомый объём. Тогда его объём равен 181.
следовательно, это искомый объём. Тогда его объём равен 181.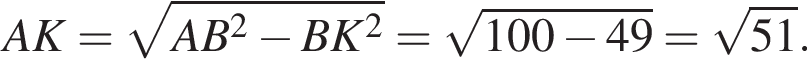
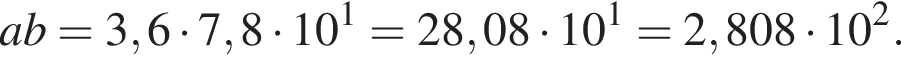
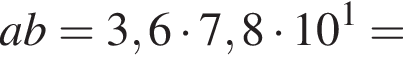
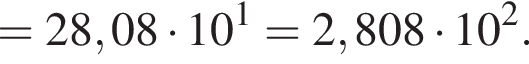
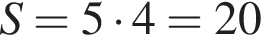 см2.
см2.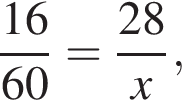 где x — неизвестное число.
где x — неизвестное число.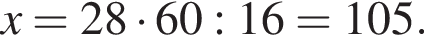
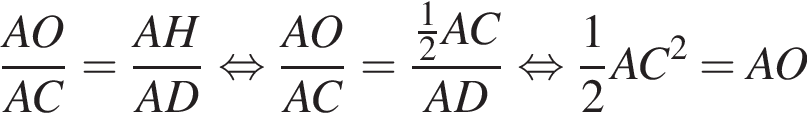
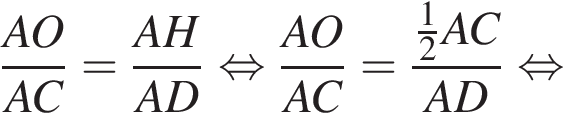
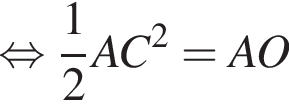

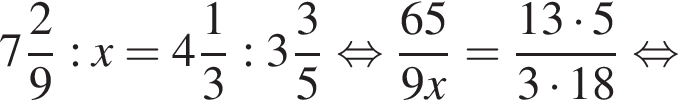
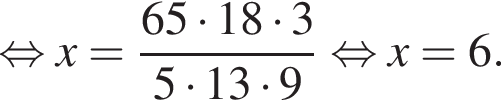
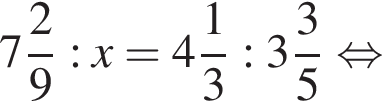
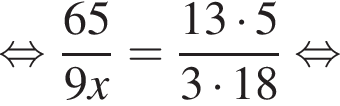
 равна 360°, поэтому четвертый угол равен 160°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 20°.
равна 360°, поэтому четвертый угол равен 160°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 20°. Тогда получим:
Тогда получим: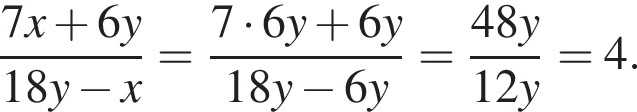
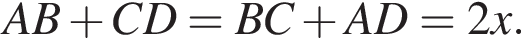 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 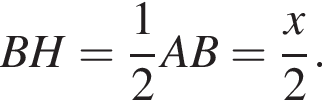 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: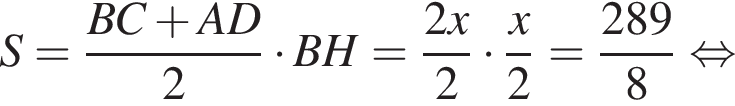
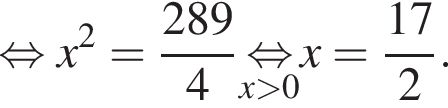
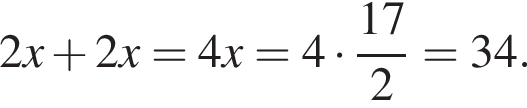
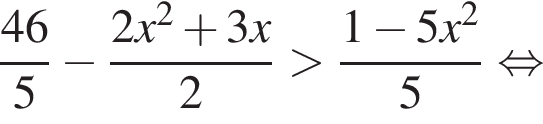
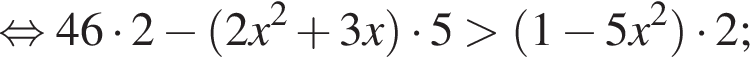
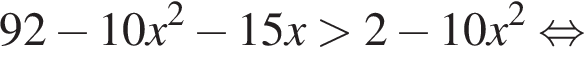

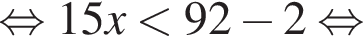

 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: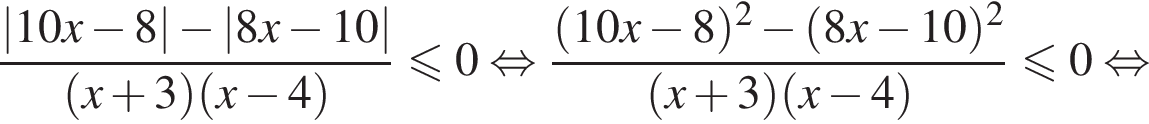
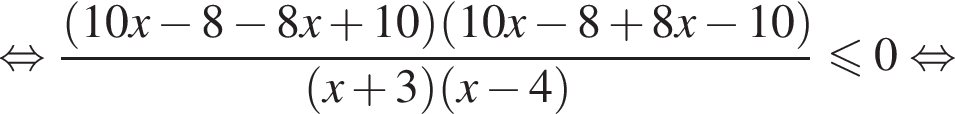
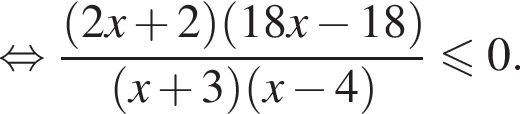
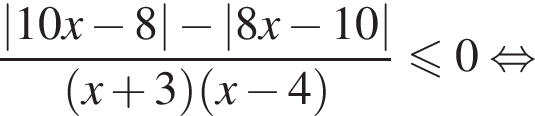
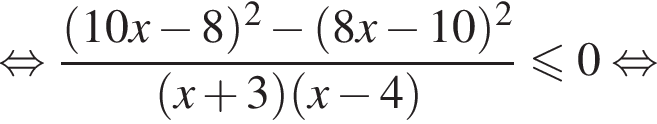
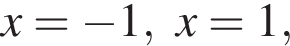 корни знаменателя
корни знаменателя 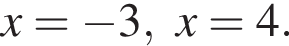 Поэтому:
Поэтому: 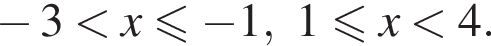 Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.
Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3. имеем:
имеем: 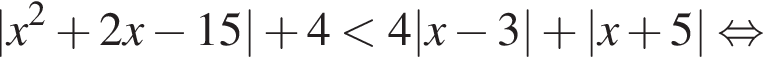
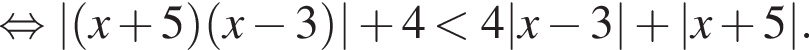
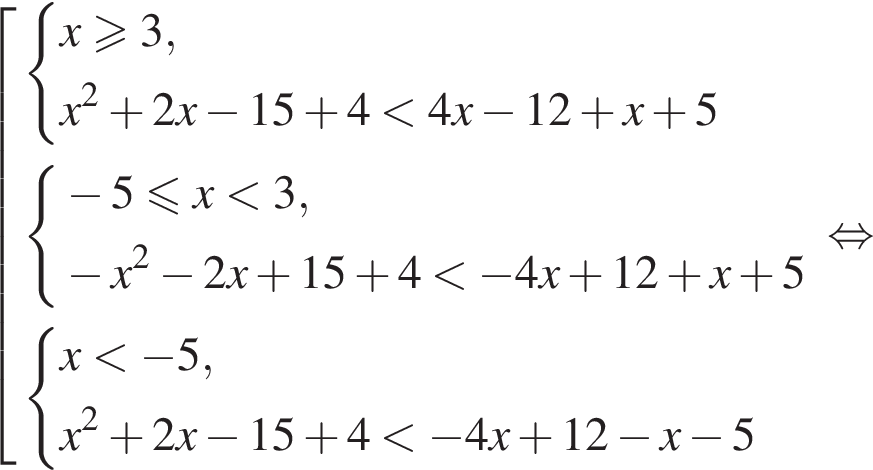
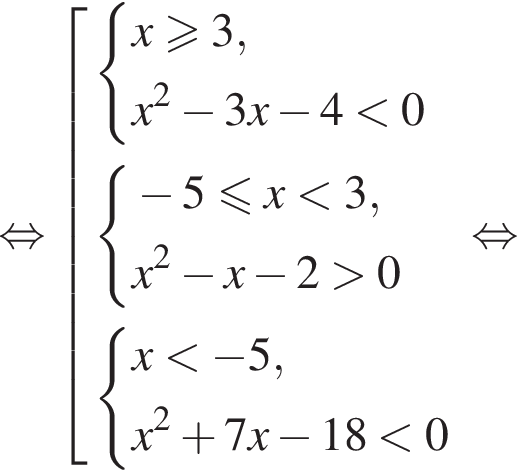
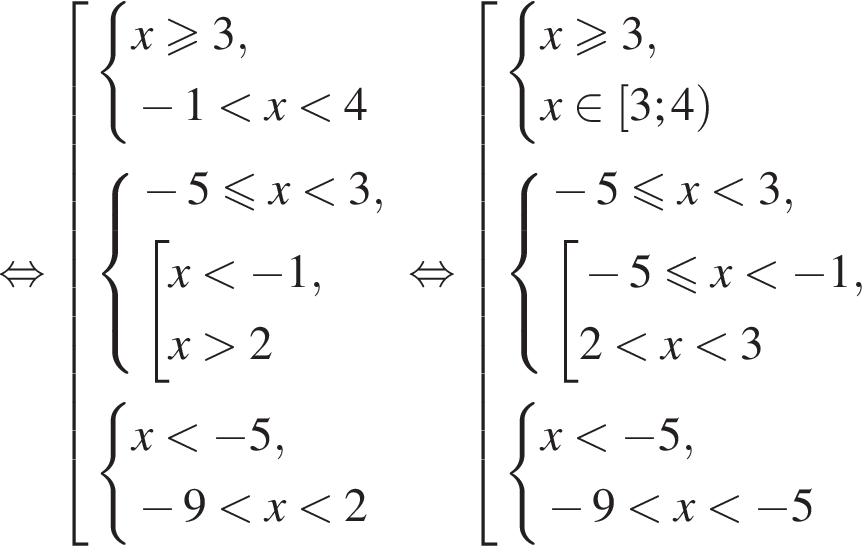
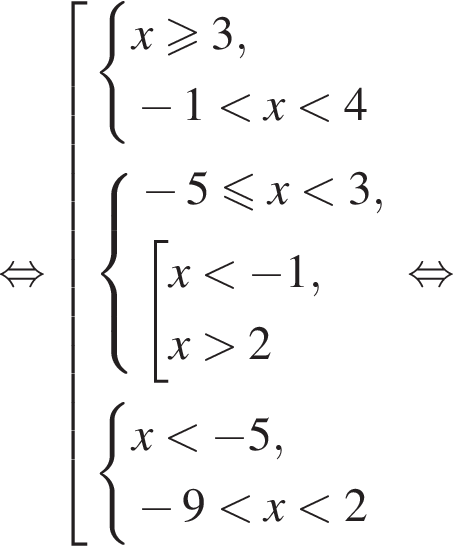
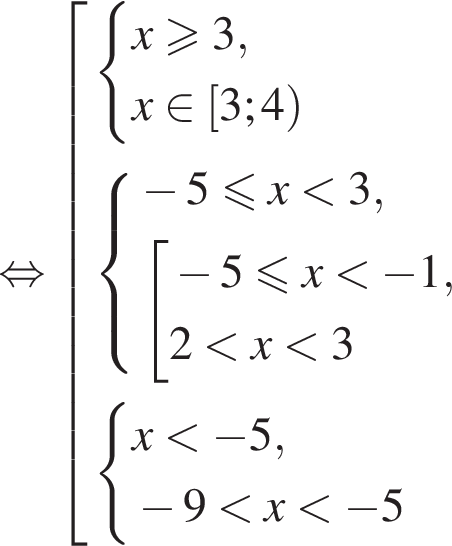
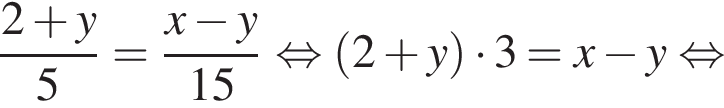
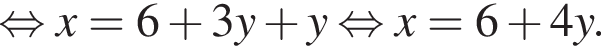
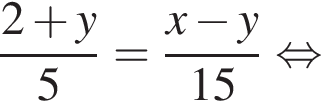
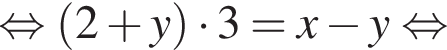


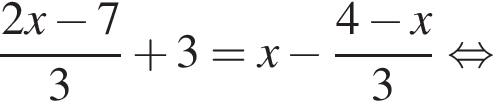
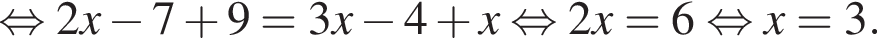

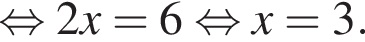
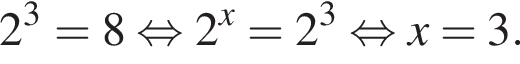
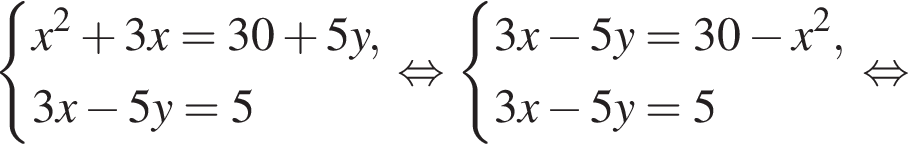
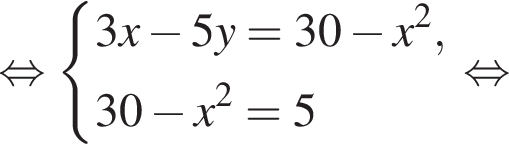
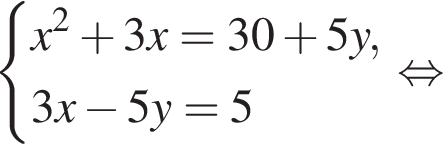
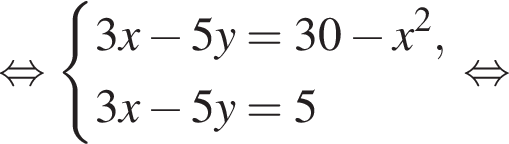
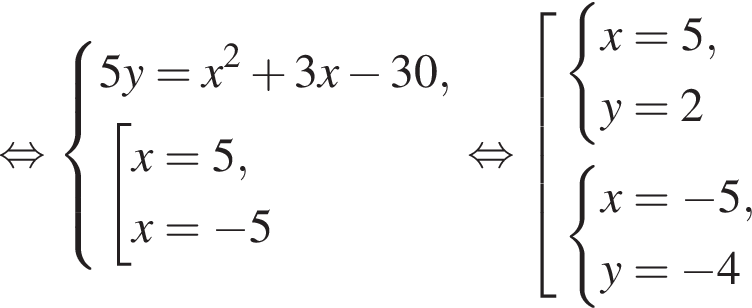

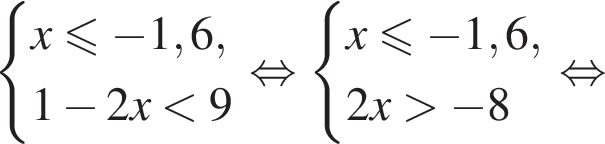
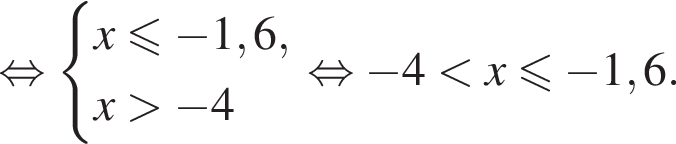
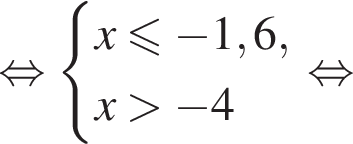
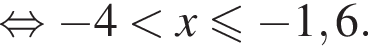
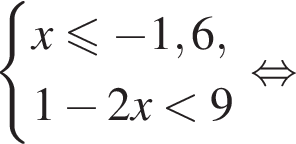
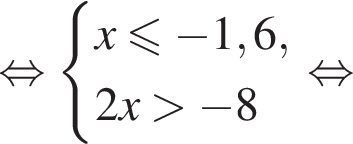
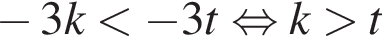 — неверно.
— неверно.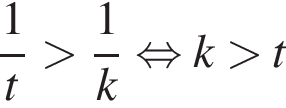 — неверно.
— неверно.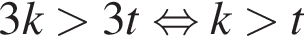 — неверно.
— неверно.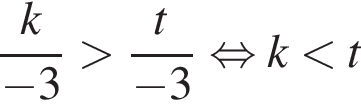 — верно.
— верно.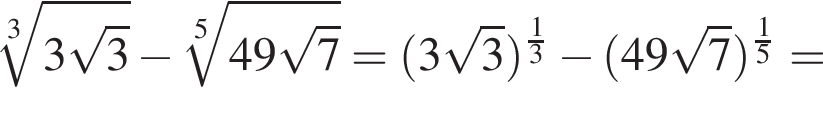
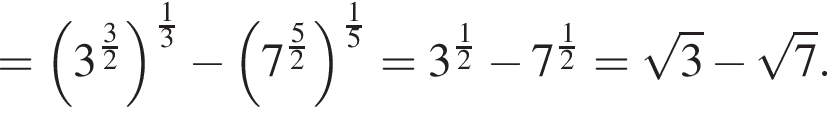
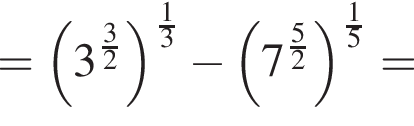
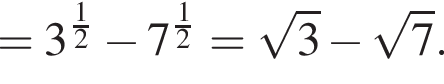
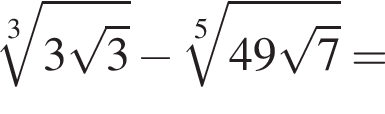
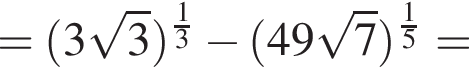
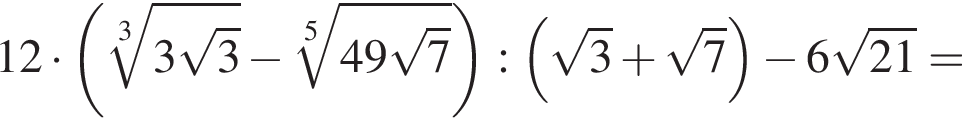
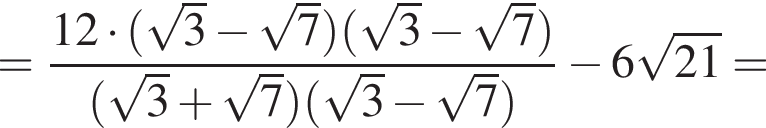
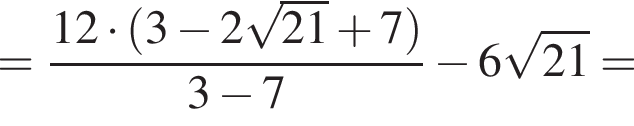
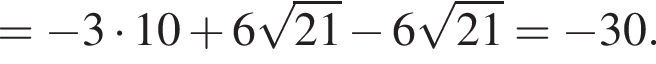

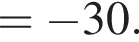
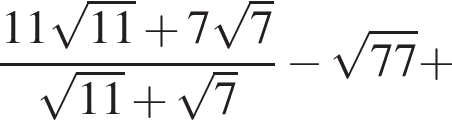
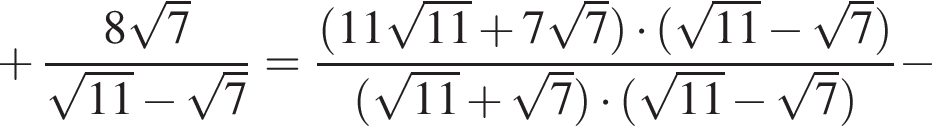
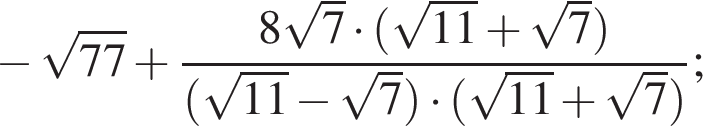

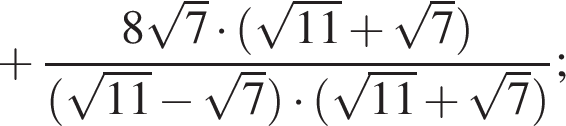
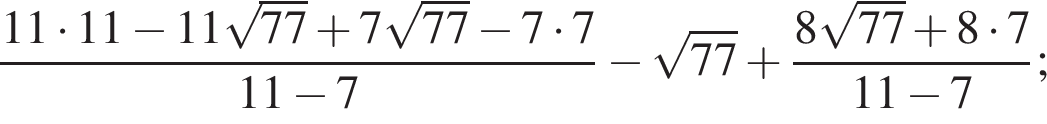
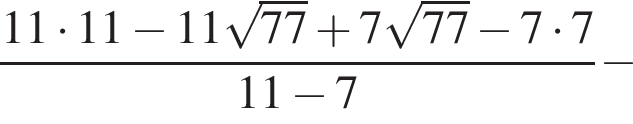
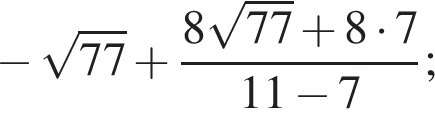
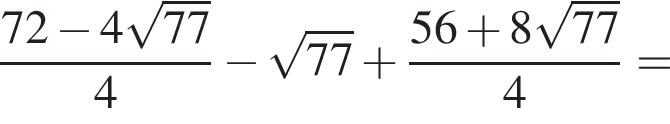
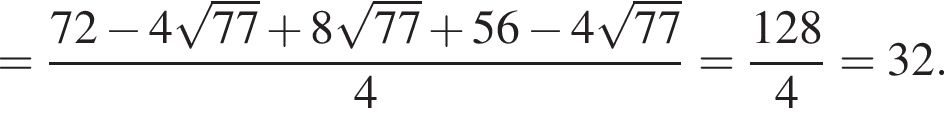
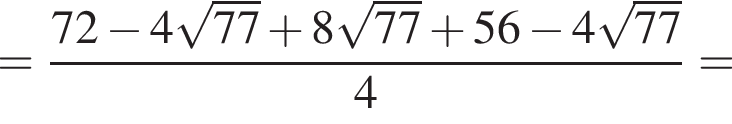
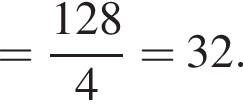
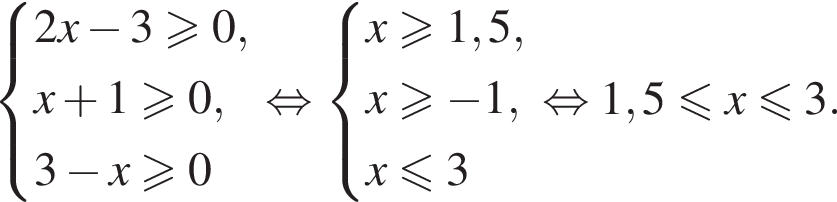
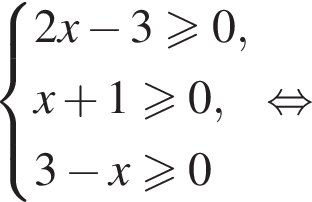
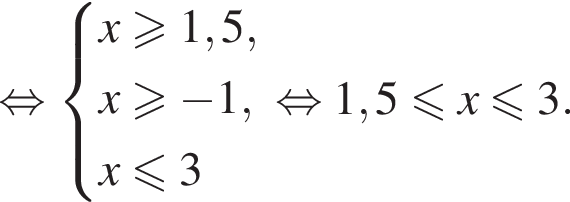
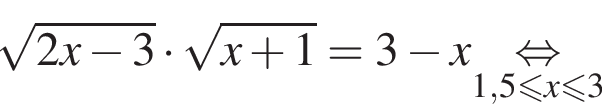
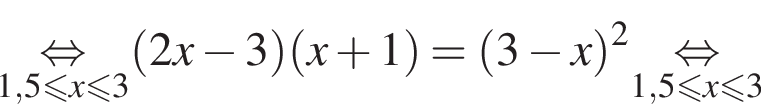
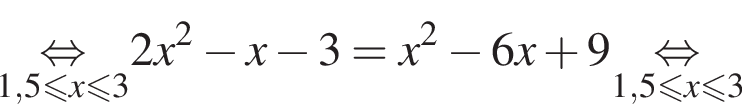
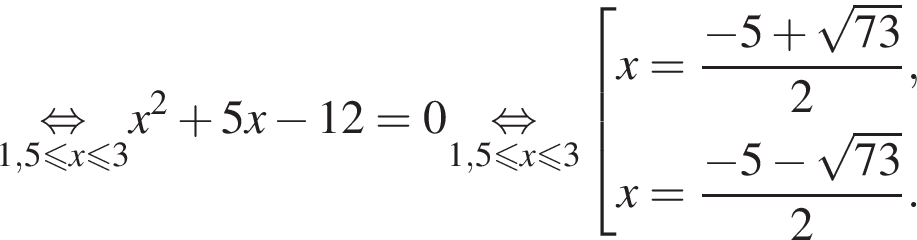
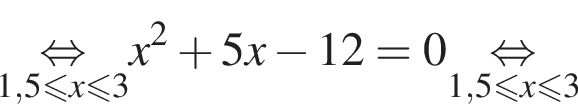
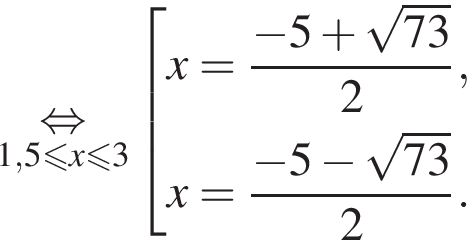
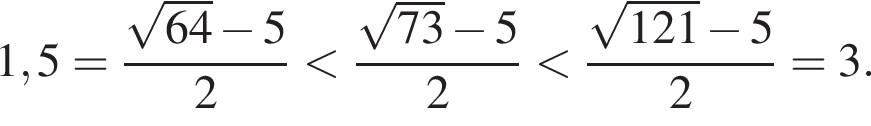
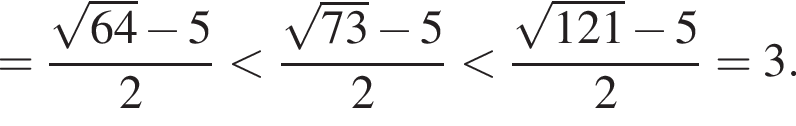
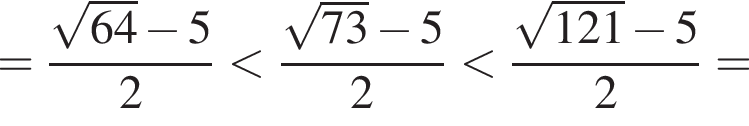
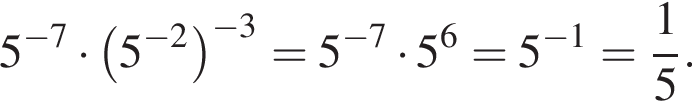

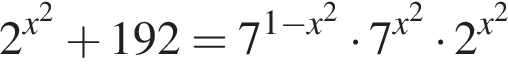
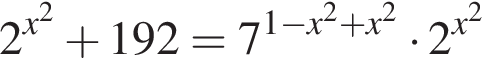
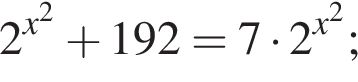
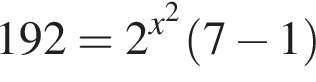
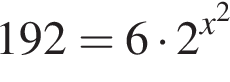
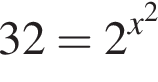
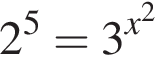
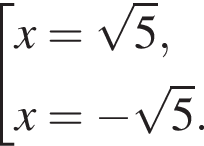
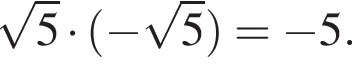
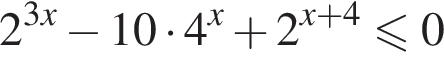
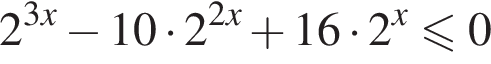
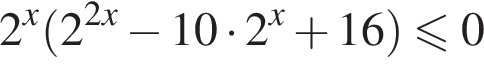
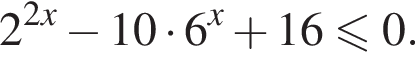
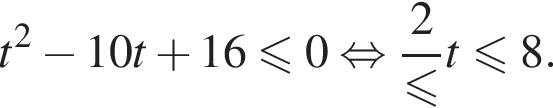
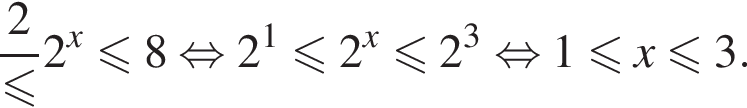
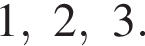 Их сумма равна 6.
Их сумма равна 6.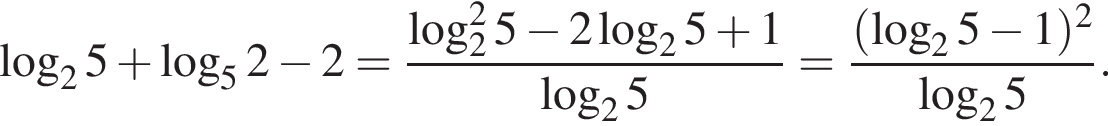
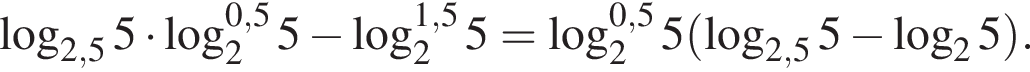
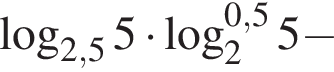
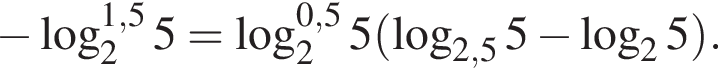
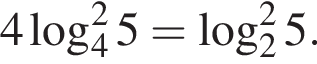 Тогда имеем:
Тогда имеем: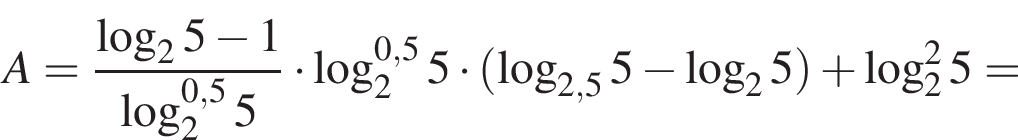
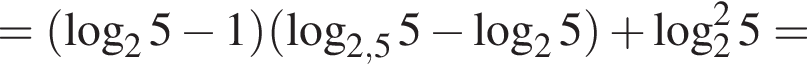
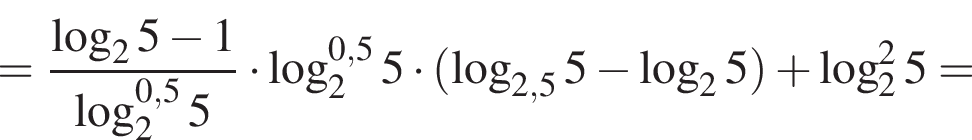
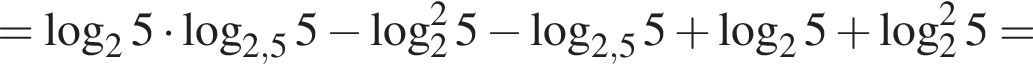
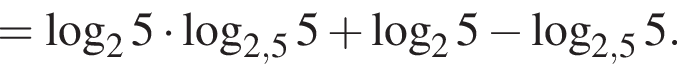
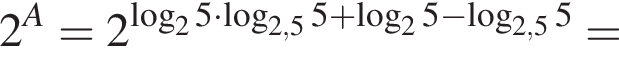
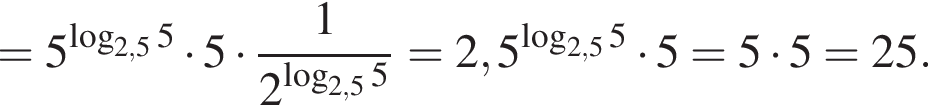
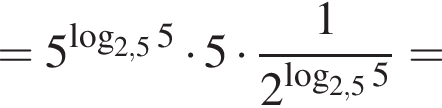
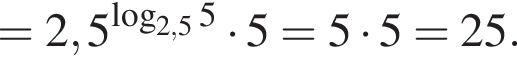
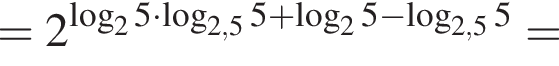
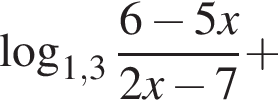
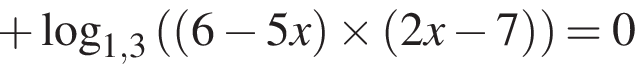
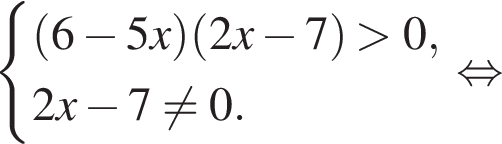
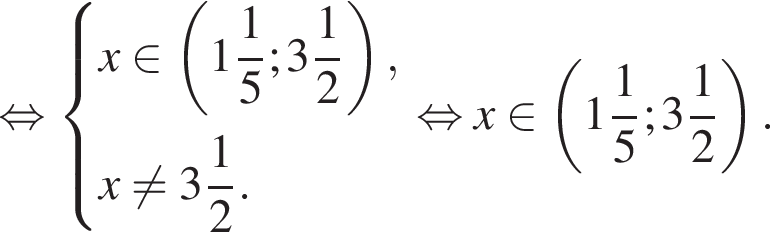
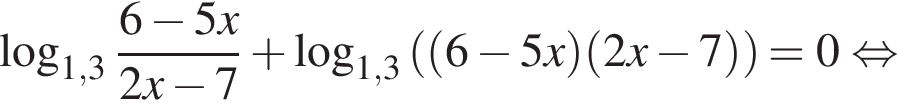
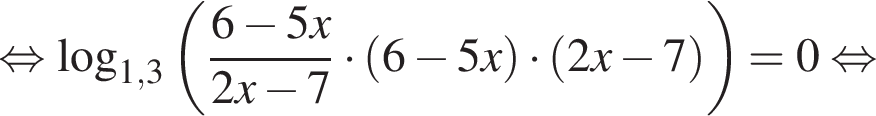
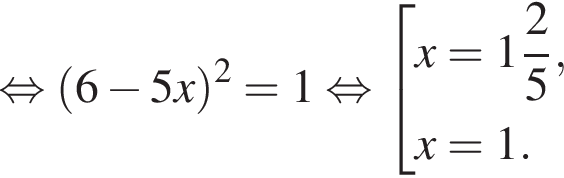
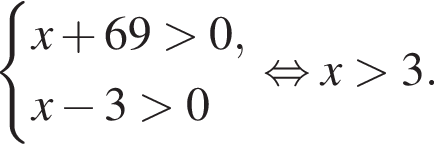
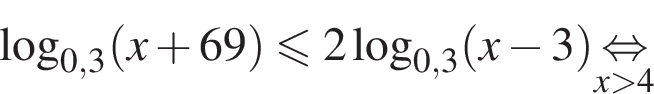
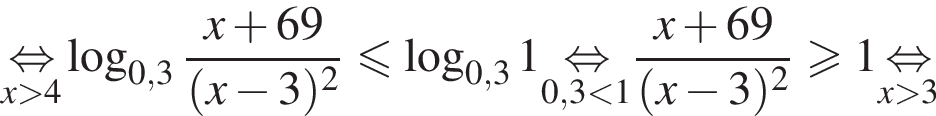
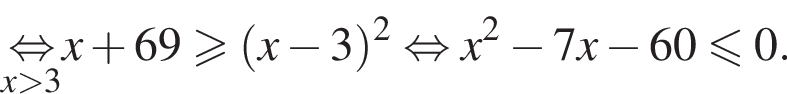
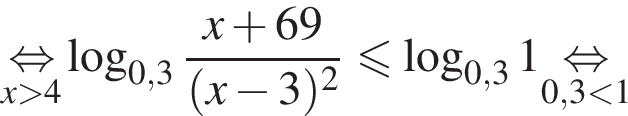
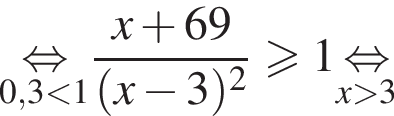
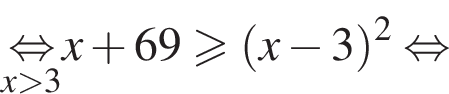
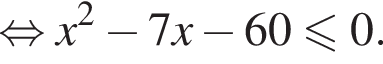
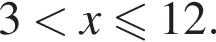 Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.
Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.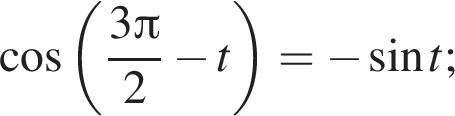
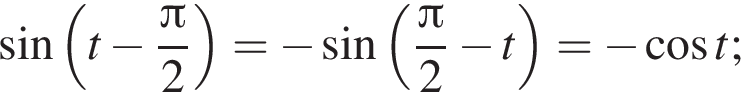
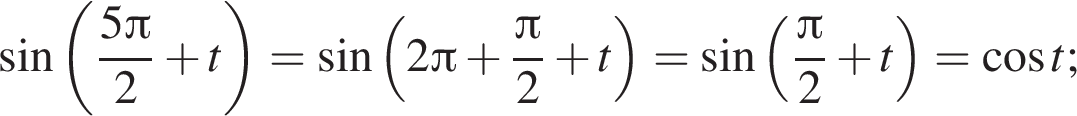
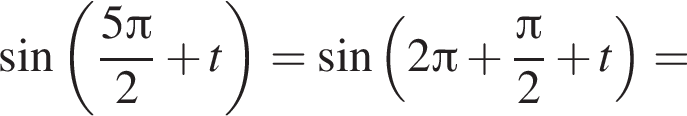
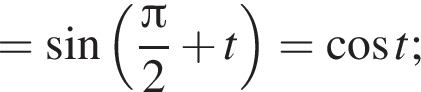
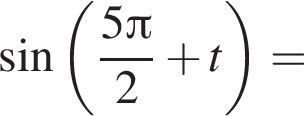
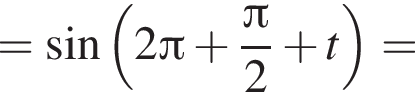
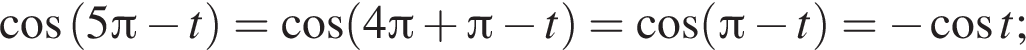

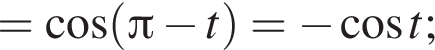
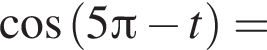
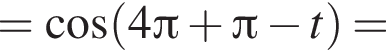
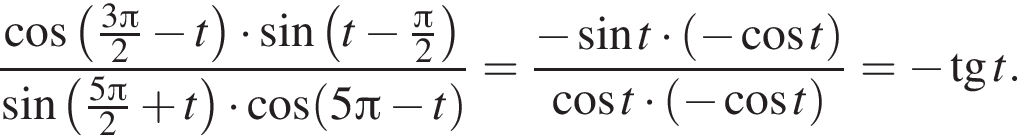
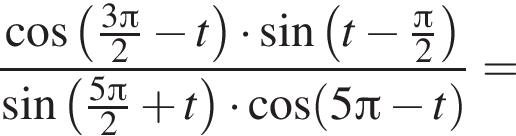
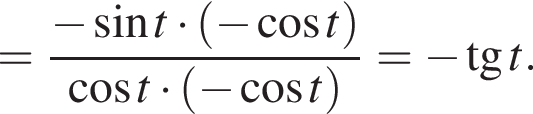
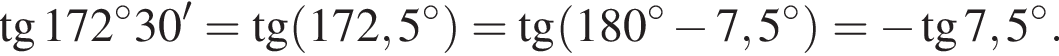
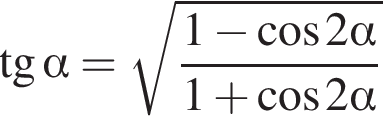 :
: 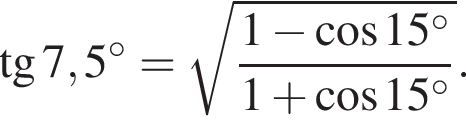



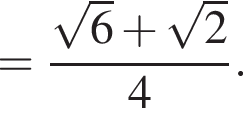
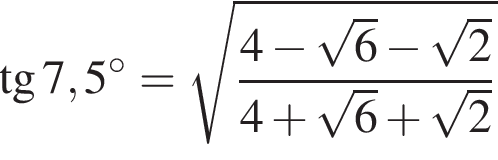
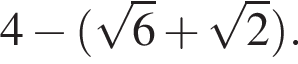 Тогда:
Тогда: 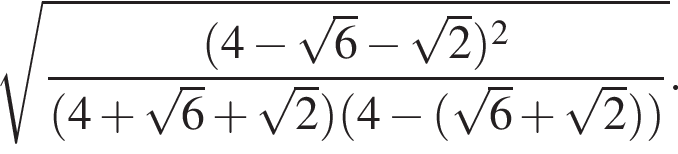
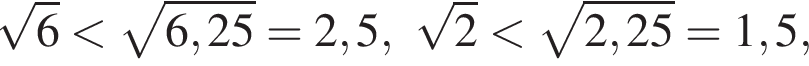
 тогда
тогда 
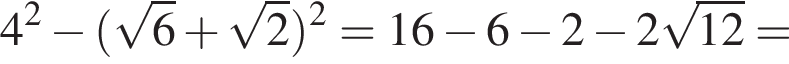

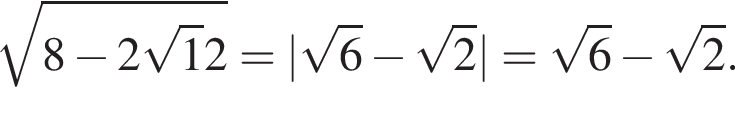 Тогда:
Тогда: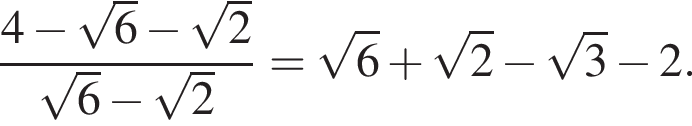
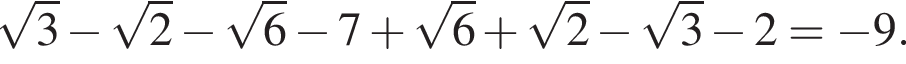
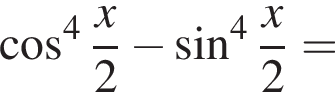
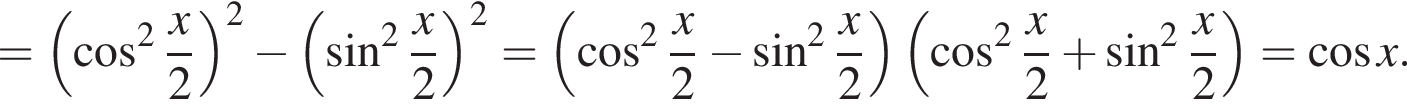
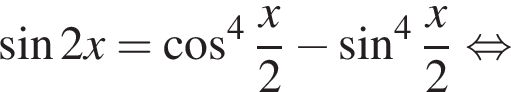
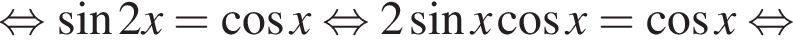
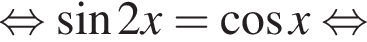

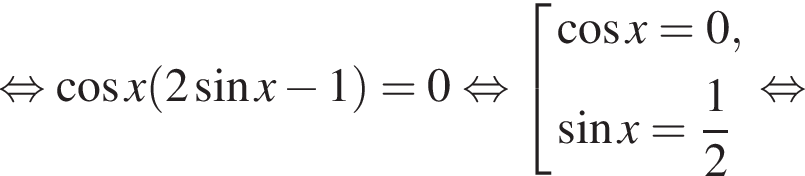
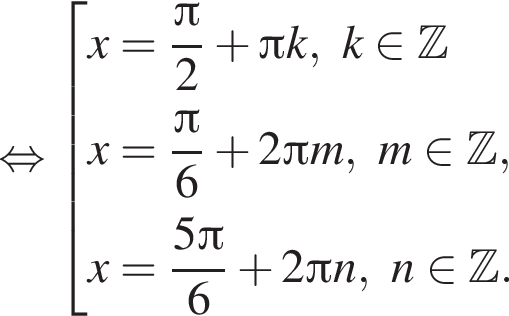
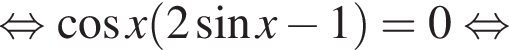
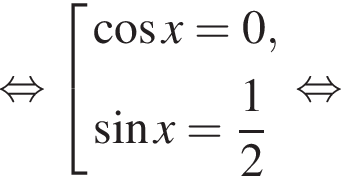
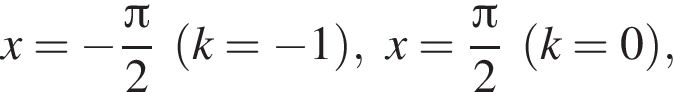
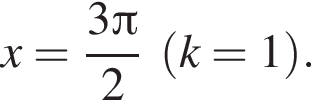 Их сумма равна
Их сумма равна 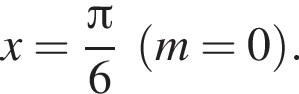 Их сумма равна
Их сумма равна 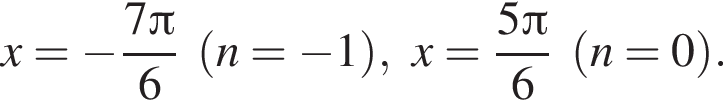 Их сумма равна
Их сумма равна 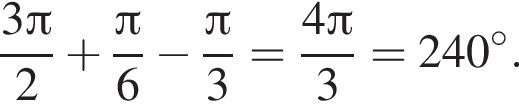

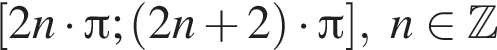 вплоть до
вплоть до 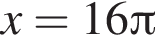 решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.
решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.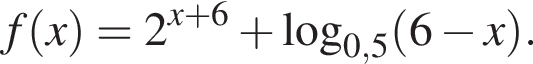 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 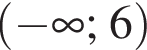
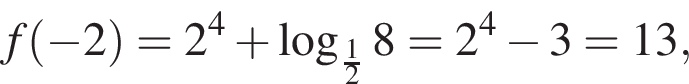 неравенство верно для всех x из
неравенство верно для всех x из 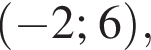 который содержит 7 целых чисел:
который содержит 7 целых чисел: 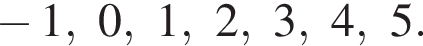
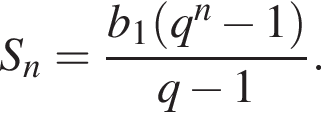 Выразим b1:
Выразим b1: 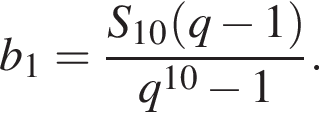 Вспомним, что
Вспомним, что 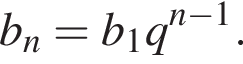
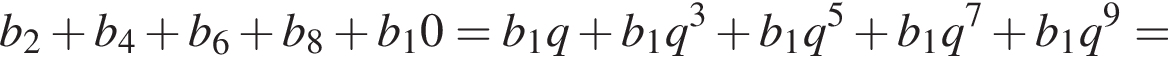
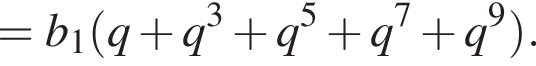
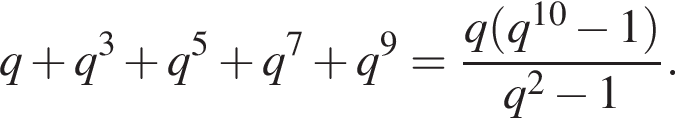 Найдем сумму членов с четными номерами согласно формуле:
Найдем сумму членов с четными номерами согласно формуле: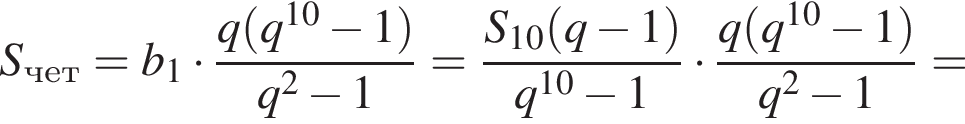
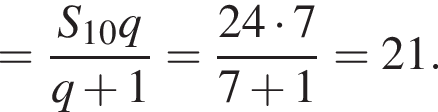
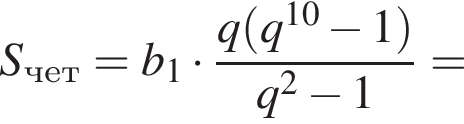
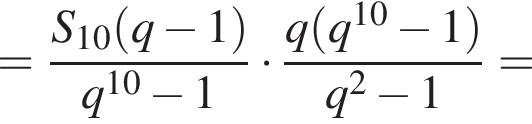
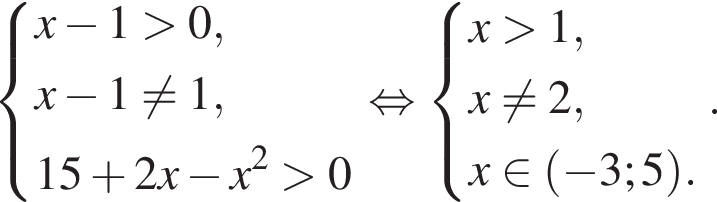
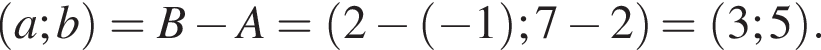
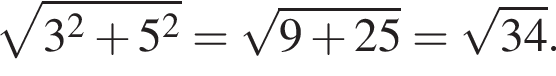 Таким образом, периметр квадрата равен:
Таким образом, периметр квадрата равен: 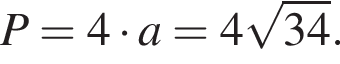
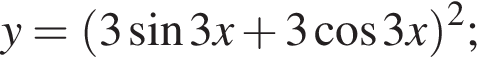


 имеем:
имеем:

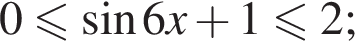
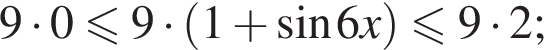
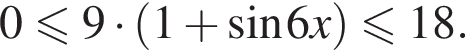
 Тогда:
Тогда: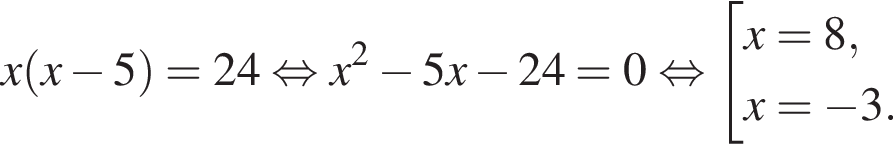
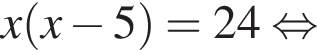
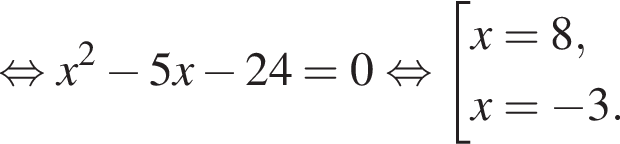

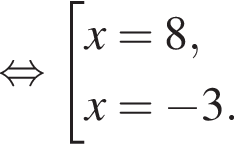
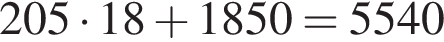 тыс. руб.
тыс. руб.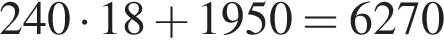 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб.